The Trillion Dollar Equation
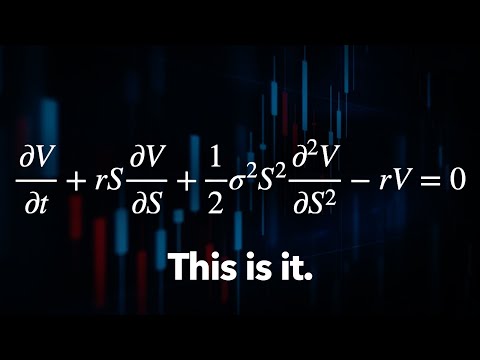
- This single equation spawned four multi-trillion dollar industries and transformed everyone's approach to risk. Do you think that most people are aware of the size, scale, utility of derivatives? - No. No idea. - But at its core, this equation comes from physics, from discovering atoms, understanding how heat is transferred, and how to beat the casino at blackjack.
So maybe it shouldn't be surprising that some of the best to beat the stock market were not veteran traders, but physicists, scientists, and mathematicians. In 1988, a mathematics professor named Jim Simons set up the Medallion Investment Fund, and every year for the next 30 years, the Medallion fund delivered higher returns than the market average, and not just by a little bit, it returned 66% per year. At that rate of growth, $100 invested in 1988 would be worth $8.4 billion today. This made Jim Simons easily the richest mathematician of all time.
But being good at math doesn't guarantee success in financial markets. Just ask Isaac Newton. In 1720 Newton was 77 years old, and he was rich. He had made a lot of money working as a professor at Cambridge for decades, and he had a side hustle as the Master of the Royal Mint. His net worth was £30,000 the equivalent of $6 million today.
Now, to grow his fortune, Newton invested in stocks. One of his big bets was on the South Sea Company. Their business was shipping enslaved Africans across the Atlantic. Business was booming and the share price grew rapidly. By April of 1720, the value of Newton's shares had doubled.
So he sold his stock. But the stock price kept going up and by June, Newton bought back in and he kept buying shares even as the price peaked. When the price started to fall, Newton didn't sell.
He bought more shares thinking he was buying the dip. But there was no rebound, and ultimately he lost around a third of his wealth. When asked why he didn't see it coming, Newton responded, "I can calculate the motions of the heavenly bodies, but not the madness of people."
So what did Simons get right that Newton got wrong? Well, for one thing, Simons was able to stand on the shoulders of giants. The pioneer of using math to model financial markets was Louis Bachelier, born in 1870. Both of his parents died when he was 18 and he had to take over his father's wine business. He sold the business a few years later and moved to Paris to study physics, but he needed a job to support himself and his family and he found one at the Bourse, The Paris Stock Exchange. And inside was Newton's "madness of people" in its rawest form. Hundreds of traders screaming prices, making hand signals, and doing deals.
The thing that captured Bachelier's interest were contracts known as options. The earliest known options were bought around 600 BC by the Greek philosopher Thales of Miletus. He believed that the coming summer would yield a bumper crop of olives.
To make money off this idea, he could have purchased olive presses, which if you were right, would be in great demand, but he didn't have enough money to buy the machines. So instead he went to all the existing olive press owners and paid them a little bit of money to secure the option to rent their presses in the summer for a specified price. When the harvest came, Thales was right, there were so many olives that the price of renting a press skyrocketed. Thales paid the press owners their pre-agreed price, and then he rented out the machines at a higher rate and pocketed the difference. Thales had executed the first known call option. A call option gives you the right, but not the obligation to buy something at a later date for a set price known as the strike price.
You can also buy a put option, which gives you the right, but not the obligation to sell something at a later date for the strike price. Put options are useful if you expect the price to go down. Call options are useful if you expect the price to go up. For example, let's say the current price of Apple stock is a hundred dollars, but you expect it to go up.
You could buy a call option for $10 that gives you the right, but not the obligation to buy Apple stock in one year for a hundred dollars. That is the strike price. Just a little side note, American options can be exercised on any date up to the expiry, whereas European options must be exercised on the expiry date. To keep things simple, we'll stick to European options. So if in a year the price of Apple stock has gone up to $130, you can use the option to buy shares for a hundred dollars and then immediately sell them for $130.
After you take into account the $10 you paid for the option, you've made a $20 profit. Alternatively, if in a year the stock prices dropped to $70, you just wouldn't use the option and you've lost the $10 you paid for it. So the profit and loss diagram looks like this. If the stock price ends up below the strike price, you lose what you paid for the option. But if the stock price is higher than the strike price, then you earn that difference minus the cost of the option.
There are at least three advantages of options. One is that it limits your downside. If you had bought the stock instead of the option and it went down to $70, you would've lost $30. And in theory, you could have lost a hundred if the stock went to zero.
The second benefit is options provide leverage. If you had bought the stock and it went up to $130, then your investment grew by 30%. But if you had bought the option, you only had to put up $10. So your profit of $20 is actually a 200% return on investment.
On the downside, if you had owned the stock, your investment would've only dropped by 30%, whereas with the option you lose all 100%. So with options trading, there's a chance to make much larger profits, but also much bigger losses. The third benefit is you can use options as a hedge. - I think the original motivation for options was to figure out a way to reduce risk. And then of course, once people decided they wanted to buy insurance, that meant that there are other people out there that wanted to sell it or a profit, and that's how markets get created. - So options can be an incredibly useful investing tool, but what Bachelier saw on the trading floor was chaos, especially when it came to the price of stock options.
Even though they had been around for hundreds of years, no one had found a good way to price them. Traders would just bargain to come to an agreement about what the price should be. - Given the option to buy or sell something in the future, it seems like a very amorphous kind of a trade.
And so coming up with prices for these rather strange objects has been a challenge that's plagued a number of economists and business people for centuries. - Now, Bachelier, already interested in probability, thought there had to be a mathematical solution to this problem, and he proposed this as his PhD topic to his advisor Henri Poincaré. Looking into the math of finance wasn't really something people did back then, but to Bachelier's surprise, Poincaré agreed. To accurately price an option, first you need to know what happens to stock prices over time. The price of a stock is basically set by a tug of war between buyers and sellers.
When more people wanna buy a stock, the price goes up. When more people wanna sell a stock, the price goes down. But the number of buyers and sellers can be influenced by almost anything, like the weather, politics, new competitors, innovation and so on. So Bachelier realized that it's virtually impossible to predict all these factors accurately. So the best you can do is assume that at any point in time the stock price is just as likely to go up as down and therefore over the long term, stock prices follow a random walk, moving up and down as if their next move is determined by the flip of a coin. - Randomness is a hallmark of an efficient market.
By efficient economists typically mean that you can't make money by trading. - The idea that you shouldn't be able to buy an asset and sell it immediately for a profit is known as the Efficient Market Hypothesis. - The more people try to make money by predicting the stock market and then trading on those predictions, the less predictable those prices are.
If you and I could predict the stock market tomorrow, then we would do it. We would start trading today on stocks that we thought were gonna go up tomorrow. Well, if we did that, then instead of going up tomorrow, they would go up now as we bought more and more of the stock. So the very act of predicting actually affects the quality of the future outcomes.
And so in a totally efficient market, the prices tomorrow can't possibly have any predictive power. If they did, we would've taken advantage of it today. - This is a galton board.
It's got rows of pegs arranged in a triangle and around 6,000 tiny ball bearings that I can pour through the pegs. Now, each time a ball hits a peg, there's a 50 50 chance it goes to the left or the right. So each ball follows a random walk as it passes through these pegs, which makes it basically impossible to predict the path of any individual ball. But if I flip this over, what you can see is that all the balls together always create a predictable pattern. That is a collection of random walks creates a normal distribution.
It's centered around the middle because the number of paths a ball could take to get here is the greatest. And the further out you go, the fewer the paths a ball could take to get there. Like if you want to end up here, well the ball would have to go left, left, left, left all the way down. So there's only one way to get here, but to get into the middle, there are thousands of paths that a ball could take.
Now, Bachelier believed a stock price is just like a ball going through a galton board. Each additional layer of pegs represents a time step. So after a short time, the stock price could only move up or down a little, but after more time, a wider range of prices is possible.
According to Bachelier the expected future price of a stock is described by a normal distribution, centered on the current price which spreads out over time. Bachelier realized he had rediscovered the exact equation which describes how heat radiates from regions of high temperature to regions of low temperature. This was first discovered by Joseph Fourier back in 1822. So Bachelier called his discovery the radiation of probabilities. Since he was writing about finance, the physics community didn't take any notice, but the mathematics of the random walk would go on to solve an almost century old mystery in physics. In 1827, Scottish botanist Robert Brown was looking at pollen grains under the microscope, and he noticed that the particles suspended in water on the microscope slide were moving around randomly.
Because he didn't know whether it was something to do with the pollen being living material, He tested non-organic particles such as dust from lava and meteorite rock. Again, he saw them moving around in the same way. So Brown discovered that any particles, if they were small enough, exhibited this random movement, which came to be known as Brownian motion. But what caused it remained a mystery. 80 years later in 1905, Einstein figured out the answer.
Over the previous couple hundred years, the idea that gases and liquids were made up of molecules became more and more popular. But not everyone was convinced that molecules were real in a physical sense. Just that the theory explained a lot of observations. The idea led Einstein to hypothesize that Brownian motion is caused by the trillions of molecules hitting the particle from every direction, every instant. Occasionally, more will hit from one side than the other, and the particle will momentarily jump. To derive the mathematics, Einstein supposed that as an observer we can't see or predict these collisions with any certainty.
So at any time we have to assume that the particle is just as likely to move in one direction as an another. So just like stock prices, microscopic particles move like a ball falling down a galton board, the expected location of a particle is described by a normal distribution, which broadens with time. It's why even in completely still water, microscopic particles spread out. This is diffusion. By solving the Brownian motion mystery. Einstein had found definitive evidence that atoms and molecules exist.
Of course, he had no idea that Bachelier had uncovered the random walk five years earlier. By the time Bachelier finished his PhD, he had finally figured out a mathematical way to price an option. Remember that with a call option, if the future price of a stock is less than the strike price, then you lose the premium paid for the option. But if the stock price is greater than the strike price, you pocket that difference and you make a net profit if the stock has gone up by more than you paid for the option. So the probability that an option buyer makes a profit is the probability that the price increases by more than the price paid for it, which is the green shaded area. And the probability that the seller makes money is just the probability that the price stays low enough that the buyer doesn't earn more than they paid for it.
This is the red shaded area. Multiplying the profit or loss by the probability of each outcome, Bachelier calculated the expected return of an option. Now how much should it cost? If the price of an option is too high, no one will wanna buy it. Conversely, if the price is too low, everyone will want to buy it. Bachelier argued that the fair price is what makes the expected return for buyers and sellers equal.
Both parties should stand to gain or lose the same amount. That was Bachelier's insight into how to accurately price an option. When Bachelier finished his thesis, he had beaten Einstein to inventing the random walk and solved the problem that had eluded options traders for hundreds of years.
But no one noticed. The physicists were uninterested and traders weren't ready. The key thing missing was a way to make a ton of money.
Hey, so I'm not sure how stock traders sleep at night with billions of dollars riding on the madness of people, but I have been sleeping just fine, thanks to the sponsor of this video, Eight Sleep. I've recently moved to Australia and it has been really hot, but I've been keeping cool at night using the Eight Sleep Pod. It's a smart mattress cover that can control the temperature of the bed and track how well you sleep. You can set the temperature to whatever you like from around 13 degrees Celsius, all the way up to 43 degrees Celsius, and my wife likes it a little warmer than I do, so it's useful that we can each have our own temperature on our own side of the bed. And if you don't know what works best for you, well the Pod will learn your ideal temperature and optimize it throughout the night using its autopilot. And usually that means getting a couple of degrees cooler during the start of the night and then warming up in the morning to help you wake up.
You can also have it wake you with a slight vibration, which is really pleasant and it doesn't disturb your partner like an annoying phone sound. You know, I've been tracking my sleep before and after using the Pod, and I've found that I've been sleeping longer and waking up less since using the Pod. So if you wanna try it out for yourself, click on the link in the description and thanks again to Eight Sleep for sponsoring this part of the video. In the 1950s, a young physics graduate, Ed Thorpe, was doing his PhD in Los Angeles, but a few hours drive away, Las Vegas was quickly becoming the gambling capital of the world, and Thorpe saw a way to make a fortune. He headed to Vegas and sat down at the blackjack table, back then, the dealer only used a single deck of cards, so Thorpe could keep a mental note of all the cards that had been played as he saw them.
This allowed him to work out if he had an advantage. He would bet a bigger portion of his funds when the odds were in his favor and less when they weren't. He had invented card counting.
This is a remarkable innovation, considering blackjack had been around in various forms for hundreds of years, and for a while this made him a lot of money. But the casinos got wise to his strategy and they added more decks of cards to the game to reduce the benefit of card counting. So Thorpe took his winnings to what he called the biggest casino on Earth: the stock market.
He started a hedge fund that would go on to make a 20% return every year for 20 years, the best performance ever seen at that time. And he did it by transferring the skills he honed at the blackjack table to the stock market. Thorpe pioneered a type of hedging, a way to protect against losses with balancing or compensating transactions. - Thorpe did it mathematically.
He looked at the odds of winning and losing and decided that under certain conditions you can actually tilt the odds in your favor by using certain patterns to be able to make bets. - Suppose Bob sells Alice a call option on a stock, and let's say the stock has gone up, so now it's in the money for Alice. Well now for every additional $1, the stock price goes up, Bob will lose $1, but he can eliminate this risk by owning one unit of stock.
Then if the price goes up, he would lose $1 from the option but gain that dollar back from the stock. And if the stock drops back outta the money for Alice, he sells the stock so he doesn't risk losing any money from that either. This is called dynamic hedging.
It means Bob can make a profit with minimal risk from fluctuating stock prices. A hedge portfolio pi at any one time will offset the option V with some amount of stock delta. - It basically means I can sell you something without having to take the opposite side of the trade. And the way to think about it is I have synthetically manufactured an option for you.
I've created it out of nothing by doing dynamic trading. Dynamic hedging. - As we saw with Bob's example delta, the amount of stock he has to hold, changes depending on current prices. Mathematically, it represents how much the current option price changes with a change in the stock price.
But Thorpe wasn't satisfied with Bachelier's model for pricing options. I mean, for one thing, stock prices aren't entirely random. They can increase over time if the business is doing well or fall if it isn't. Bachelier's model ignored this.
So Thorpe came up with a more accurate model for pricing options, which took this drift into account. - I actually figured out what this model was back in the middle of 1967, and I decided that I would just use it for myself and then later I kept it quiet for my own investors. The idea was to basically make a lot of money out of it for everybody. - His strategy was if the option was going cheap, according to his model, buy it. If it was overvalued, short sell it, that is bet against it. And that way, more often than not, he would end up on the winning side of the trade.
This lasted until 1973. In that year, Fischer Black and Myron Scholes came up with an equation that changed the industry. Robert Merton independently published his own version, which was based on the mathematics of stochastic calculus, so he is also credited. - I thought I'd have the field to myself, but unfortunately, Fischer Black and Myron Scholes published the idea and they did a better job of the model than I did because they had very tight mathematics behind their derivation - Like Bachelier, they thought that option prices should offer a fair bet to both buyers and sellers, but their approach was totally new. They said if it was possible to construct a risk-free portfolio of options and stocks just like Thorpe was doing with his delta hedging, then in an efficient market, a fair market, this portfolio should return nothing more than the risk-free rate, what the same money would earn if invested in the safest asset, US treasury bonds.
The assumption was that if you're not taking on any additional risk, then it shouldn't be possible to receive any extra returns. To describe how stock prices change over time, Black, Scholes, and Merton used an improved version of Bachelier's model just like Thorpe. This says that at any time we expect the stock price to move randomly, plus a general trend up or down, the drift. By combining these two equations, Black, Scholes, and Merton came up with the most famous equation in finance. It relates the price of any kind of contract to any asset, stocks, bonds, you name it. The same year they published this equation, the Chicago Board Options Exchange was founded.
Why is that equation so important? Like for finance, how did that change the game? - Well, because when you solve that partial differential equation, you get an explicit formula of the price of the option as a function of a bunch of these input parameters. And for the very first time, you now have an explicit expression where you plug in the parameters and out pops this number so that people can actually use it to trade on. - This led to one of the fastest adoptions by industry of an academic idea in all of the social sciences. - Within just a couple of years, the Black Scholes formula was adopted as the benchmark for Wall Street for trading options.
The exchange traded options market has exploded and it's now a multi-trillion dollar industry, the volume in this market has been doubling roughly every five years. So this is the financial equivalent of Moore's Law. There are other businesses that have grown just as quickly, like credit default swaps market, the OTC derivatives market, the securitized debt market.
All of these are multi-trillion dollar industries that in one form or another make use of the idea of Black Scholes Merton option pricing. - This opened up a whole new way to hedge against anything, and not just for hedge funds. Nowadays, pretty much every large company, governments, and even individual investors use options to hedge against their own specific risks. Suppose you're running an airline and you're worried that an increase in oil prices would eat into your profits. Well, using the Black Scholes Merton equation, there's a way to accurately and efficiently hedge that risk. You price an option to buy something that tracks the price of oil, and that option will pay off if oil prices go up, and that will help compensate you for the higher cost of fuel you have to pay.
So Black Scholes Merton can help reduce risk, but it can also provide leverage. - An ongoing battle between bullish day traders and hedge fund short sellers that have bet against the stock, GameStop shares, have now risen some 700%. - Well, GameStop is a really interesting example for all sorts of reasons, but options figured prominently in that example because a small cadre of users on this Reddit sub-channel r/wallstreetbets decided that the hedge fund managers that were shorting the stock and betting that the company would go out of business needed to be punished. And so they bought shares of GameStop stock to try to drive up price. Turns out that buying the stock was not enough, because with a dollar's worth of cash, you can buy a dollar's worth of stock, but with a dollar's worth of cash, you can buy options that affected many more than a dollar's worth of stock, perhaps in some cases $10 or $20 worth of stock for a dollar's worth of options.
And so there's natural leverage embedded in these securities. And so the combination of buying both the stock and the options caused the prices to rise very quickly. And what that did was to cause these hedge fund managers to lose a lot of money quickly. - How big is this market for derivatives? How big is this whole area that kind of comes out of Black Scholes Merton? - There are estimates of how large derivatives markets are, and first, let's be clear what a derivative is. A derivative is a financial security whose value derived from another financial security. So an option is an example of a derivative.
In general, the size of derivative markets globally is the on the order of several hundred trillion dollars. - How does that compare to the size of the underlying securities they're based on? - It's multiples of the underlying securities. - I just have to interrupt because it seems kind of crazy that you have more money riding on the things that are based on the thing than the thing itself. - That's right. - So tell me how that makes any sense. - Because what options allow you to do is to take the underlying thing and turn it into 5, 10, 20, 50 things.
So these pieces of paper that we call options and derivatives, they basically allow us to create many, many different versions of the underlying asset, versions that individuals find more palatable because of their own risk reward preferences. - Does this make the markets and the global economy more stable, or less stable, or no effect? - All three. So it turns out that during normal times, these markets are a very significant source of liquidity and therefore stability. During abnormal times, by that I mean when there are periods of market stress, all of these securities can go in one direction, typically down, and when they go down together, that creates a really big market crash. So in those circumstances, derivatives markets can exacerbate these kinds of market dislocations. - In 1997, Merton and Scholes were awarded the Nobel Prize in economics.
Black was acknowledged for his contributions, but unfortunately he had passed away just two years earlier. - We were gonna make a lot of money in options, but now Black and Shoals have told everybody what the secret is. - With the option pricing formula now out for everyone to see hedge funds would need to discover better ways to find market inefficiencies. Enter Jim Simons.
Before Simons had any exposure to the stock market, he was a mathematician. His work on Riemann geometry was instrumental in many areas of mathematics and physics, including knot theory, quantum field theory, and quantum computing Chern Simon's theory laid the mathematical foundation for string theory. In 1976, the American Mathematical Society presented him with the Oswald Veblen Prize in geometry.
But at the top of his academic career, Simons went looking for a new challenge. When he founded Renaissance Technologies in 1978, his strategy was to use machine learning to find patterns in the stock market. Patterns provide opportunities to make money. - The real thing was to gather a tremendous amount of data and we had to get it by hand in the early days, we went down to the Federal Reserve and copied interest rate histories and stuff like that 'cause it didn't exist on computers.
- His rationale was that the market is far too complex for anyone to be able to make predictions with certainty. But Simons had worked for the US Institute for Defense Analysis during the Cold War, breaking Russian codes by extracting patterns from masses of data. Simons was convinced that a similar approach could beat the market. He then used his academic contacts to hire a bunch of the best scientists he could find.
- What was your employment criteria then? If they knew nothing about finance, what were you looking for in them? Someone with a PhD in physics and who'd had five years out and had written a few good papers and was obviously a smart guy or in astronomy or in mathematics or in statistics. Someone who had done science and done it well. - It's not surprising that mathematicians and physicists are involved in this field. First of all, finance pays a lot better than, you know, being an assistant professor of mathematics. And for a number of mathematicians, the beauty of option pricing is equally compelling to anything else that they're doing in their professions.
- One of these was Leonard Baum, a pioneer of Hidden Markov models. Just as Einstein realized that although we can't directly observe atoms, we can infer their existence through their effect on pollen grains, Hidden Markov models aim to find factors that are not directly observable, but do have an effect on what we can observe. And soon after that, Renaissance launched their now-famous Medallion fund. Using hidden Markov models and other data driven strategies, The Medallion fund became the highest returning investment fund of all time. This led Bradford Cornell of UCLA, in his paper Medallion Fund: The Ultimate Counterexample? to conclude that maybe the efficient market hypothesis itself is wrong. - In 1988, I published a paper testing it, the US Stock Market, and what I found was that the hypothesis is false.
You can actually reject the hypothesis in the data. And so there are predictabilities in the stock market. - So it's possible to beat the market is what you're saying. - It's possible to beat the market if you have the right models, the right training, the resources, the computational power, and so on and so forth, yes.
- The people who have found the patterns in the stock market, and the randomness for that matter, have often been physicists and mathematicians, but their impact has gone beyond just making them rich. By modeling market dynamics, they've provided new insight into risk and opened up whole new markets. They've determined what the accurate price of derivatives should be, and in doing so, they have helped eliminate market inefficiencies. Ironically, if we are ever able to discover all the patterns in the stock market, knowing what they are will allow us to eliminate them. Then we will finally have a perfectly efficient market where all price movements are truly random.
2024-03-02 15:41


