Quantum Noir Session 3: Quantum Technologies
Professor Will Oliver, who is the Harry Willis Herron Professor of Electrical Engineering and Computer Science at Lincoln Labs as part of MIT. And he will tell us about giant artificial atoms and molecules chiral photon emissions via quantum electrodynamics. Yeah. Thanks, James. Really appreciate the introduction. And thanks, Bill, for the invitation.
Really glad to be here and talk about some of our research that we're doing in the engineering quantum systems group. Before I get started, let me recognize some collaborators in Nakamura's group in Japan, also Franco Nori, Anton Kockum there in-- also in Japan and Sweden now, and Yariv Yanay and Charlie Tahan. And I'd like to talk about some experiments with superconducting qubits, but we're going to call them artificial atoms, and in fact, we'll call them giant artificial atoms.
So to define that terminology, let's think about what a small atom is. That's the usual atoms that we think about. They're small in the sense that if we wanted to drive a transition in the atom, the atom itself in its spatial extent is small compared to the wavelength of the light that we're using to drive it. So this allows us to make the dipole approximation. And you can think of it as an atom or a qubit connected to a control volume in one place only. And most of the atoms that we think about in life are this way.
So if you have a natural atom from the periodic table, it's about an angstrom. We drive it with optical light, maybe 100 to 1,000 nanometers. And so the ratio of those two is 1 in 1000, 1 in 10,000.
Now these things called Rydberg atoms, where you excite the atom to a highly excited state makes it much, much larger. And you might think, OK, that's a giant atom, but in fact, it's even deeper in the small atom regime, because when we have that large atom, now 10 to 100 nanometers, we're now driving it in the microwaves. And if you look at that ratio, it's now 1 in 10,000 to 1 in 1,000,000, so even smaller.
Superconducting qubits, though, you can see them with your eye. So they're quite large, 100 microns. And we also drive them in the microwave.
And nonetheless, you take this ratio, it's 1 in 100, 1 in 1,000. So a superconducting qubit is also a small atom. But we have some flexibility with superconducting qubits in that we can make them look like giant atoms.
So giant atom meaning its spatial extent couples to the wave that's driving it in more than one place or in multiple places. And we can do that because we basically make electrical circuits. So we can draw wires from our qubit to the control line and connect it in different places. And now you think about trying to drive this atom, the dipole approximation doesn't work. Classically, the atom is not following the electric field anymore. How does it follow it? Because it's coupled to it in multiple places.
Which one do I follow? So this, of course, leads to quantum interference, self-interference, and it means dipole approximation is no longer valid. So what we're going to do is we're going to leverage the large size of superconducting qubits, our ability to connect it in multiple places and quantum interference to realize high fidelity operations in waveguide QED. That's what we want to do. So the first topic will be waveguide QED and giant artificial atoms.
Just the initial demonstration. And this is work done by Bharath Kannan, who's now CEO of Atlantic Quantum, a startup, and Dan Campbell, who is a postdoc and is now at AFRL in Rome. So superconducting artificial atoms are basically qubits, but they start off life as an LC circuit. And this is a harmonic oscillator. You might recognize this as parallel LC circuit with a resonance frequency 1 over the square root of LC. And if you cool this down to low temperatures, in fact, it is a harmonic oscillator and so it will have discrete energy levels, and those levels correspond to counting the number of excitations of this circuit.
So this doesn't happen at room temperature but if you cool it down enough, this is a quantum circuit. But it's not a qubit. And the reason it's not a qubit is because the transitions between 01, 12, 23, they're all degenerate, right? And so I can't live only in the 0, 1 subspace without exciting all the levels.
So what we need to do is something else. And that something else is to introduce a nonlinear element. Here, it's called a Josephson junction.
And for the purposes of this talk, it's just a non-linear inductor. It's two superconducting leads separated by a thin insulating barrier. And Brian Josephson basically gave us these two constituent relationships for the current and the voltage of this device. And when we combine them in the usual way to form a-- to define the inductance, we find the inductance is non-linear in the current that flows through that device. So it is a non-linear inductor. You could even calculate the energy and find out that it depends on the phase as a cosine.
And so if we make that same LC circuit using the nonlinear inductor, we find now that the potential profile, rather than being quadratic or harmonic, is in fact a cosine. And what that means is that the 0, 1 transition frequency now differs from the 1, 2 and the 2, 3. OK. So now we can live in just the 0, 1 subspace, drive that transition without exciting higher levels if we're careful. OK. So many artificial atoms are built from this concept.
This one is called the fixed frequency transmon. And we're going to use a variant of that in these experiments. Now, the second term to introduce is waveguided QED, and that is a variant in some sense of cavity QED. So cavity QED has been used in quantum information for a long time, and it's basically a way to protect atoms from this environment. And the way that we protect it is by putting it inside a cavity. Now, in the environment, there's a quasi continuum of modes that would love to take the energy from my atom.
And one way to protect it is by putting it in a cavity, I now have discrete set of energy levels. Now, if my atom is on resonance with one of those energy levels, I actually enhance the spontaneous emission, happens faster. That's called Purcell effect. But if I tune my atom from those cavity modes, I'm actually protected, and we take advantage of that in superconducting quantum computing in particular. It is the dominant architecture today to protect qubits from their environment so that they're long lived. OK.
So then you might say, well, that sounds great. Why are we going to go back to waveguides? Waveguides seem like a really bad idea. Because I'm coupling qubits directly to a waveguide, which has a quasi continuum of modes, which wants to take the energy away. And the reason is that our application that we're interested in is to make a quantum interconnect.
We want the qubit to emit a photon. We want it to emit it quickly, go down a waveguide to another place and get absorbed again. We're making an interconnect for qubits or for qubit processors.
And in that case, we don't want the cavity mirrors there because that's going to just interrupt-- --a photon will bounce around many times before it actually leaves. OK. But there's no free lunch. In waveguide QED, we have some challenges. So one is that there's an always on dissipation, it's always trying to take energy away.
How do we control our qubits in the presence of that dissipation but still do something useful? And then the second question is, can we engineer interactions that are mediated by this waveguide also while avoiding the dissipation's? And we will answer these two questions. OK. So maybe one more thing about coupling atoms to propagating photons. If you are in free space and you have an atom and you want to drive it, you could think of driving it with a plane wave. And the plane wave would excite the atom or the qubit from the ground to the first excited state. And then when it emits, it emits spherically.
It emits in all directions. And what we find is that, well, OK, this looks very pretty. It's an interference pattern between the incoming and the outgoing waves, but it's not so practical. And what we would say is that this is a poor spatial mode matching. What's coming in doesn't look anything like what's going out.
And if I wanted to capture all those photons, I need two position detectors everywhere in there. OK. Now, with superconducting qubits, we have an advantage in that we're coupling it to a one-dimensional waveguide, and that means there's really only two directions to go, forwards and backwards. And so if we drive this qubit coupled to this waveguide, we send in a wave this way, it excites the qubit. The qubit will emit a photon which goes backwards and forwards. That's every direction from a one-dimensional perspective.
And what we find is that if we're in the one photon or less than one photon limit at a time arriving at this atom-- --the forward scattering is completely suppressed by quantum interference and the reverse scattering is enhanced. And this is just to say that there is a big advantage to working in one dimension. OK. Now you might wonder, what about cooperativity? Can we get into the strong coupling limit? Well, in the case of cavity QED, of course, you have the enhancement of the cavity, and you also have the matrix element.
But we don't have a cavity, right? So you could just think of that as one, order one. But with superconducting qubits, we can basically couple it as strongly as we want to this waveguide. And so we can still enter the strong coupling limit where exchange of energy between the qubit and the waveguide, that rate is much larger than, say, any other non-radiative relaxation time.
So we are in the strong coupling limit. OK. So with that, the experiment we do looks something like this. We've got qubits, and we'll couple them to our waveguide. They exchange energy at a rate gamma.
The qubit frequency is omega, and then it, of course, loses energy to other degrees of freedom, not just the waveguide. Getting one step closer, you could schematic this as a qubit. Now you see here, there's two Josephson junctions forming a squid-- --and we do that because by putting a magnetic field through that loop, we can tune the qubits frequency. That's useful.
When it's at 20 millikelvin in a fridge, we would like to be able to have a knob at room temperature to change its frequency. OK. But otherwise, you can see that this is an inductor in parallel with a capacitor and it's coupled to a 50 ohm transmission line illustrated here as a coax cable but that's not what we're going to use. What we actually use is a coplanar waveguide.
It's a center strip. Here's ground. So the center signal line is in black.
There's silicon field in white, and then the ground plane is also in black. So that's the coplanar waveguide. We capacitively coupled to it from our qubit. This is the capacitor of our qubit.
It's a lateral capacitor. It's side by side, not parallel plate. And then zooming in here, you can see this is our inductor, which is in the squid format. And we put a magnetic field through it to tune the qubit frequency. So that is our device.
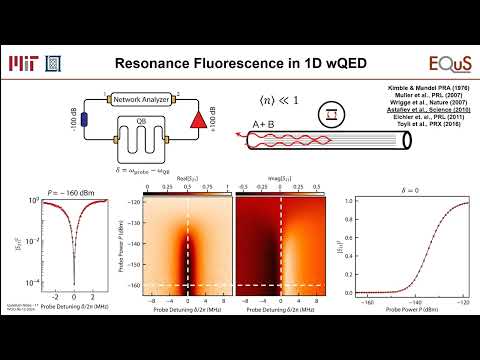
OK. So just to show that this all works, what we can do is at 20 millikelvin, we have our qubit chip. Here's the waveguide, couples to a qubit. And at room temperature, we have a network analyzer and that will send a signal out port one, comes in here, interacts with the qubit, and then the signal continues, gets amplified and goes to port two. But remember, what I said is that if we're not too strong of a field, the average photon is less than one, then all of the energy should be reflected, which means none of it should pass through and arrive at port two when we're on resonance. And that's exactly what we see.
So what we're doing is that 0 here is the detuning so it's on resonance. And when we're on resonance and we look at what arrives at port two, it's less than 1 part in 10,000, almost nothing arrives there. Detune it just a little bit and now a lot of photons are going through because they're not absorbed by the atom. And you can look at this in a 2D plot where we're plotting the detuning as well as the probe power. And this dashed line here is what we're taking.
I won't explain too much about that, but just to say that, yeah, OK, if we're on resonance and we increase the power that we're applying, eventually, we start to see energy appearing at the second port because basically more than one photon is arriving. While the atom is interacting with the first photon, a bunch of other ones just run right by and end up at port two of my network analyzer. So this is all working the way we expect. OK. So let's make it one level more complicated. We're going to braid two of these giant atoms.
We have two qubits, a and b, and we attach them or couple them to the waveguide at specific points, and we can define the distance between these points in terms of phase. So what is that phase? Well, it's the physical distance between the qubits, that's delta x, divided by the velocity of a photon at that frequency here, it's about a third the speed of light, times the frequency of that photon, which is same as the frequency of the qubit that emits it. OK. This is what the circuit looks like on a chip. The two qubits are in yellow shown here.
And then the blue is the waveguide and it meanders back and forth, but you can see that it hits each qubit twice before it leaves, right? So each qubit is coupled twice to that waveguide and they're interleaved. OK. And if we zoom in, this is the capacitor. It's a different shape than the square I showed before, but it's still the capacitor coupled to the waveguide in two places. We can control the frequency. We had a feature here where just for experimental control, we used a conventional way to read it out as well just to double check.
But that's not part of the experiment. OK. So the first thing we can demonstrate is that we can basically turn off dissipation to the 50 ohm environment. So we terminate these in 50 ohms. It's a 50 ohm waveguide.
We're going to forget about qubit b for a moment. We'll just detune him in frequency. And we're just looking at what happens with qubit a. We'll put qubit a in its excited state. And when we do that, it can emit a photon and that can happen in a few different ways.
One way is that it could just emit from this point to the 50 ohm environment. OK. Or it could emit on this side instead, and the photon has to travel all the way around to get to the 50 ohm environment, and it picks up a phase of 2 phi in doing that. So this basically starts to look like an interferometer. And if I pick the correct phase, I could have this process destructively interfere quantum mechanically so that it doesn't happen. OK.
And remember, that phase is determined by the frequency of my qubit. Now, you might say, oh, there's another 50 ohms over here. That's true, but the process works in either direction. And so by picking the right phase, you basically can turn down the dissipation, this is the decay rate gamma 1, to the 50 ohm environment. And what we see is that it's minimum at this one point and if we detune the frequency, then of course it's going to increase because this destructive interference is no longer perfect. OK.
And if you prefer to look at things in the time domain, here's the decay traces, this T1, the longest was about 30 microseconds in this case, which is consistent with a qubit that wasn't coupled to any waveguide at all. OK. And then as we detune the frequency, it gets larger and larger or the T1 goes down the decay rate. OK. So we answered the first question.
We can, in fact, turn off the dissipation to the environment. Now, the second question is, can we couple these qubits together while also being decoupled from the environment? And so I won't go into the physics behind this today but just to say that these qubits do couple to each other, and they couple in this way. It's of course related to the rate at which they're coupled to the waveguide, turns out it's gamma over 2, times sine of this phase and pairs of points will couple, right? So here are two points between a and b, another two points between a and b and another two points between a and b. And then of course, there's one more pair, the outermost, and they're separated by 3 phi rather than 1 phi, but they all have this same gamma over 2 in front. Now this is a coherent quantum mechanical process.
So each of these paths will add together. And so the net coupling strength is actually all four of these paths. OK. Now if we take one of the qubits, hold it at a fixed frequency, take the other qubit and sweep its frequency, when they're on resonance with each other, they interact and an avoided crossing opens up.
Of a strength here, it's 2g over 2 pi. OK. So they do, in fact, interact with one another via the waveguide but what's quite interesting is that coupling can occur over quite a range of frequencies, including the one where they don't see the 50 ohm environment. So we're interacting two qubits with one another via the waveguide, but they don't see the 50 ohm termination. So this is quite useful.
OK. So we can engineer this coupling spectrum in a few other ways. First is the number of coupling points. We just looked at a qubit coupled at two points, and it had one minimum in the decay rate, but I could couple it at three points. And it turns out that'll give me 2 minima, four points will give me 3 minima, et cetera.
OK, so that's one thing I can do. Another thing I could do is these coupling strengths need not all be the same. I could tune them relative to one another and the impact that, that has, the ratio of gamma 2 to 1 one where this is gamma 2, you can see that by increasing that ratio, if you think of that as a double well, it's suppressing the barrier. OK.
And of course, the third one is that I can move my qubits around. I don't have to have them equidistant. So in the experiment that we used to demonstrate the giant atom, we used a coupling of three. So each qubit is coupled at three points. The size of the circle here indicates the strength of the coupling, and you can see that the distances are not all equal.
Now, this is what the circuit looks like. We can have two qubits and the waveguide meanders back and forth but now it'll hit each qubit three times. OK. Coupled at three points. OK.
These are the numbers in case you're interested in terms of the phases or distance between the qubit as well as the relative strengths. And so now when we look at this, we can map out that, in fact, the decay rate now does have 2 minima as we wanted because we've coupled it three points. And if we look at the coupling between qubits when they're resonant, it can be designed to be the same at these two decoherence free frequencies.
OK. So the experiment then was let's see if we can create an entangled state. All right.
So we have two qubits, qubit a and qubit b, and we park each one at their own frequency. When they're not at the same frequency, they don't talk to each other, but each one is isolated from the environment. Well, then, OK, we start them both on the ground state. We then put a pi pulse on qubit b so it's in the excited state now.
We'll then shift the frequency of qubit a up to the frequency of qubit b. They're now on resonance, and they're going to exchange energy with one another for some period of time until we shift qubit a back down and park it at its own decoherence free spot. And then we'll do readout and ask what state are you in.
And what we find is that we get, in fact, this exchange interaction or swap type interaction between the two qubits. And you can see that by the bright spot here corresponds to a dark spot and then it toggles back and forth. So if we take a slice when they're both truly on resonance, then you can really see these oscillations, and they are juxtaposed with one another.
And to make an entangled state, the idea is to do half a swap or square root of swap, as we call it. And when we do that, we create this entangled state 01 minus i10. We can then do state tomography. And what we find is that we're able to do this with about 94% fidelity.
Now, that's not a world record. Some of the best two qubit gates are now more than three 9s with superconducting qubits. But we have to remember that these two qubits are both strongly coupled to a waveguide. If we didn't do all these tricks, it would have decayed within about 10 or 20 nanoseconds.
We wouldn't even have been able to prepare this first pi pulse with any reasonable fidelity. But we can do it because these are giant atoms, and we play these tricks. OK.
So we can entangle qubits despite the strong coupling to the open environment. And that becomes a tool that we'll now use. So the tool-- the use is to show directional photon emission so that we can send a photon deterministically to one place or another and then catch it. Now, this is worked by again, by Bharath and also by Dan.
So towards these quantum interconnects. So we would like networks of quantum modules, we like modularity, systems are built upon modules, and we need to distribute the entanglement between different modules. So there are a couple of examples of interconnects today with superconducting qubits. One is based on a cavity.
You make a cavity, you couple qubits to that cavity and the pros here are that these have given the highest fidelity so far. They are bidirectional. I can send the photon right or left, but it's limited in terms of how long this cavity can be. If I make it too long, the free spectral range goes down, the separation between cavity levels goes down, it becomes a problem. The other way you could do it is you can couple via single ended waveguide. So this is like waveguide QED.
But to get rid of the unwanted dissipation and they end up putting in one of these isolators or directional circulators and they tend to be pretty lossy and they're quite big. And this just isn't really extensible. So we were wondering is there something else that we could do based on quantum interference.
So the idea now is rather than just making a giant atom, let's make a giant molecule. OK. So the molecule comprises two artificial atoms, qubit 1 and qubit 2, and we're going to put them in an entangled state. Now I'm going to use e and g for excited and ground state. And importantly, we're going to change this phase. But let's just look at this particular example, pi over 2 phase shift.
OK. So if we couple these two or a single molecule now because it's entangled to the wave guide, but we do it at different points, then we're also going to get emission and quantum interference. And so the idea is how does that happen? Well, there are a couple different pathways by which it can happen.
So one of them is that qubit 1 was actually excited and emitted its photon and it admitted it to the right. And if we're bookkeeping how that happens, there are two phases. One is the qubit state phase. Well, this is e to the i0, so we'll just call it that. And the other is the position phase. Well, I'll just call that x equals 0.
And so now that's e to the i0 as well. And the 01 means zero photons went left, one photon went right. Of course, in an entangled state it could have been qubit two that was excited and it emits its photon and it could have gone to the right. And in that case, the phase is now e to the I pi over 2. So that appears here.
And given the convention of how we do things in physics as opposed to engineering, we're going to say that this is pi over 2 away, and it comes in with a minus sign. OK. Now, I won't talk through the leftward one, but it's the same story. Qubit 1 could have emitted that photon to the left with these phases or qubit 2 could have admitted it to the left with these phases. But what you find is that interestingly, these two perfectly and destructively interfere. So I'm only left with a photon that goes to the right.
So by choosing this phase of this entangled state of my giant molecule, I can say photon, I want you to go to the right. Now, there's one thing that you might be wondering, which is we just talked about how these two qubits coupled to each other via the waveguide. Absolutely true. And that would ruin this picture that I just described.
And so what we need to do is we need to couple qubits 1 and 2 in a controlled way that's exactly equal but opposite sign of the coupling through the waveguide. And we do that. And when we do, this simple quantum optics picture of photon emission holds. OK. So same story on the other side.
But what I do is I change this phase from plus pi over 2 to minus pi over 2. And when I do that, it's now the leftward photon that survives and the rightward photon that destructively interferes. So I have a way to deterministically send a photon either to the right or to the left. OK. So w end up doing this in what we call an emitter module.
The two qubits that I just talked about are what we'll call emitter qubits and they emit to this waveguide. But I want to prepare the entangled state and couple it to a processor node that's my future application. So I'm going to add two more qubits here, 3 and 4.
I'll create the entangled state that I then shuttle down to the waveguide, right, and then when I absorb, I'm going to bring it back in and store it here and eventually couple it to some other processor that's local to it. So I need to couple these two qubits together so that I can create an entangled state. And the idea is once I have that and I'm ready to send it to the waveguide, I'll couple 3 and 4 simultaneously down to 1 and 2.
I shift the photon down and then it goes, and it'll go left or right, depending on the phase that I chose. So this is what the device looks like. You can see these two qubits up top and pink, that's qubits 3 and 4. Their coupler is shown here. Qubits 1 and 2 are at the bottom. They're coupled to the waveguide.
Here's the coupler that nulls out any coupling via the waveguide. And then here are the two shuttle couplers. Looks a little complicated, but it actually works. Its eight qubits total. And if we want to generate a photon, this is basically what we do.
We start with all of our qubits in the ground state. We will put qubit 3 in the excited state, for example. We then drive an interaction between 3 and 4.
We'll do the square root of swap gate again and create the entangled state here. And when we want to shift it down, we drive these couplers and we shift that entanglement from the top qubits to the bottom qubits. And when they reach the bottom qubits, they then emit their photon.
In this case, it's-- let's say we chose it to go to the right. OK. So here's an example of a photon that is only going to the on right, but not to the left. And here's one where it's going to the left, but not to the right. So just to show that this works and these measurements are made at room temperature, of course.
And just to mention that we're actually measuring the voltage-- --because we want to measure these field amplitude operators so that we can then build up any order of correlation function that we want so we can do tomography. OK. So we're not measuring the power, we're measuring directly the amplitude. So we can do that tomography. You can see those correlation functions here at the bottom. And what we find is that when we send the photon to the right, by and large, that's exactly what we see, is that there's a photon on the right.
And when we send it to the left, there's a photon on the left. We do that with almost 95% or 96% fidelity. So of course, we'd like that to be 99. We're working on that.
But this is already pretty good. So the next step then is to show that this modular network works. And this is work that's done by Aziza and Beatriz. So the idea here is I don't need to have just one of these modules. I could have many of them, and they're all coupled to some local quantum processing unit. And I'd like to entangle or connect how these processing units talk to one another.
And I can do that by connecting them in an all to all manner along a single waveguide. Now, here I'm showing it linearly, but it could wind back and forth. This could be two-dimensional, could even be three-dimensional. OK. And the idea is that I'll send a photon from the emitter, and I'll send it to this module, which is the absorber.
And one nice feature of this, which is from the Nakamura group, is that all I need to do is run this one backwards from the procedure. I used to emit it, and I can absorb it. So it's the same module. I could then do a different one here.
And so any combination or pair of these can send photons to one another. OK. So in the experiment, we have two interconnected modules. This is done in kind of a first try kludgy way, but it actually worked pretty well, is we've got two modules connected by a coaxial cable, and we're going to send the photon from the left to the right, and then we'll send it from the right back to the left.
So this first module is in package 1, which is on this side of the thermal finger at the mixing chamber of a dilution refrigerator. Package 2 is on the other side. And then you can see the coax, it's a niobium titanium coax which basically just looped around and connected them together. Lots of loss in this system, lots of connections. But as a proof of principle, it worked.
Let me show you how it worked. So the first step is we want to shape the photon. This is not strictly required, but it's a bit easier to run in reverse with a symmetric photon because then it's truly just the time inverted process. So we did our best to emit a photon and make this wave packet look symmetric.
I don't know if you remember before, but it was a little bit lopsided to the right. Here, we're able to shape it and by some metric it's maybe 97%, 98% symmetric. And here's one going in the other direction. And again, it's 96-ish percent symmetric. OK. The directional absorption protocol looks like this.
We again, are going to create this entanglement up top. We have an entangled state. Now this time we simultaneously drive the entanglement down to the emitters-- --and at the same time, we're driving these couplers to absorb it back up on the other side as this photon is traveling over. OK. And then we're going to measure what happens up top. OK.
There are a lot of parameters. 73 is a matter of fact. There are six baseband frequencies.
I won't read through them all. There are a lot of parameters and Aziza and Beatriz did a lot of work tuning them by hand and then decided there's got to be a better way, and that is to use reinforcement learning, which we did. So the idea is to choose a calibration for some of these parameters that you think is at least close or maybe inspired by some physics that we know.
You then use a computer to choose another candidate. You then actually send that candidate down. You collect data, and you-- by some cost function and reward, you update a neural network, and you just keep iterating this. This is called one epoch. And as you do more and more epochs, you find that your calibration is getting better and better and better and then at some point, it saturates. So this is training this-- our reinforcement learning.
This is how we did this experiment, and it's based on this work by Leon Ding and Max Hayes, where they were able to use a similar reinforcement learning algorithm to get to qubit gate fidelities above 99.9%. Published last year. So let's look at rightward photon absorption. So we're emitting a photon from this emitter module, and we're going to absorb it on the absorber side. So the first experiment is let's not absorb it. Let's intentionally not absorb it, and we're just going to let that photon go out to our detector at room temperature.
We see it on the right. It looks pretty symmetric. Good. We don't see too much on the left, maybe a little bit here because some of it gets reflected. But by and large, we sent the photon to the right, and we detected it. The next thing is let's turn the absorber on and see what we see at room temperature.
Well, now we don't see anything on the right. And we don't see anything on the left. So it must have gone somewhere. And so what we do is we then measure these qubits. We'll first measure the qubits 3 and 4 as a function of time as they're emitting the photon.
And so they eventually relax back to zero. And then we look at qubits 7 and 8 and see how they absorb the photon and turn on. Now, ideally these should be the same. They're a little bit different. We're working on that.
And in fact, the other direction looks better, and I'll show that in a moment. But indeed, we're absorbing that photon over here now. And the maximum absorbed population was about 63%.
If we do it in the other direction and we send that photon back, now you can see that it absorbed more symmetrically on the left side and it must be related to some of the calibrations that we're doing. OK. So we can now do absorber state tomography.
So we're looking at here's a leftward photon, here's a rightward photon, and we're just doing state tomography of what's absorbed. And based on that, we can make a budget for where we have errors. So first is that there's just incoherent loss due to propagation that turns out to be about 16%. We have a lot of coaxial connectors that we would never use in a real experiment just to do this.
The decoherence gives us about 10%. We can improve that. We know we've got a directionality error of a few percent. We're working on improving the missed absorption error. Altogether, the Bell state fidelities are about 0.6.
The concurrence is also about 0.6. That's above the threshold of 0.5. These are truly two entangled modules separated on different sides of the thermal finger. OK.
And the error budget is about 32%. So roughly speaking, we're up at around 90%, 93% if we accounted for all this error. OK. So then the last experiment, and then I'll stop, which is remote entanglement, which is that we would love to entangle these two or these four qubits in the absorber and the emitter module because now we can do remote gates.
OK. So we do what I just described, except we're going to stop halfway. So rather than emitting a whole photon and absorbing that whole photon, we're going to play that trick we played before with the square root of swap gate, we're going to stop it halfway. So whether it actually went or not, that's part of the entanglement. And these four qubits are now entangled together into a W state where you can see that the one keeps shifting over one spot from qubit 8, qubit 7, qubit 4, qubit 3 all in a single state with some phases.
OK. And so when we do state tomography of that, we find that it's similarly about 62% and that's true whether we're doing it to the left or to the right. OK.
And again, so these are entangled. So this is the status as of a few weeks ago. So we're still working hard on this, and we'd like to now go to a architecture where we're not using coax cables to connect these modules, but it's all on the same chip using flip-chip bump bonding. Just to highlight this again, the two qubit gate that we have here using flux onium, we now have more than three 9's qubit gate fidelity. This is really good.
Recent results, which we're preparing now is we almost have five 9's for the single qubit gate. And I won't have time to talk about how we did that today, but it's basically by driving two quadratures at the same time. So it's basically emulating circularly polarized driving or circularly polarized light on our qubit. And this allows us to get rid of the counter-rotating term. OK. But what I do want to say is that we are also focused on larger qubit arrays.
Here's a 16 qubit device, a 4x4 array. And to-- you can see that it's getting quite crowded at the edges, all the wires that we need to get in there-- --and that's why for about 10 years we've been working on 3D integration, which is really critical if we're going to realize systems at scale. This is just a cartoon to show qubit chip, an interposer, a readout chip. And you can stack them all together using indium bump bonds in a way that protects the qubit coherence because it doesn't see anything different than it did before.
It sees more of this gray, which is high resistivity silicon. You end up getting some benefits. There's another plane to work with and superconducting through silicon vias is part of this. And so this top chip would be this. And we're doing experiments where we're doing this flip chip and it's working quite well. But I'm definitely out of time.
So let me acknowledge the team. This is the engineering quantum systems group at MIT campus and also our sister group out at MIT's Lincoln Laboratory. And let me acknowledge our many sponsors who make it possible and also thank you for your attention. [APPLAUSE] Hello.
Alejandro Ponta here. I would like to ask you a question about that 16.4 propagation loss in the coaxial cable. You hinted at it a little bit, but would be possible to pry a little bit more information on how you want to mitigate that loss over time, especially as it is connecting to different modules? Yeah, absolutely.
So that coax cable, you've got a wire bond that goes to a k connector, that goes into another k connector, and then another one, and another one, and another wire, right? So it's just death by 1,000 cuts. The way that we would want to do this in the future is to have a multi-chip module. So you basically have a platform on which we're going to place many chips and each chip is basically a module, and then we're going to talk with each other via this 3D integration that we just showed. Follow-up-- That's the idea how to get rid of that 16%. Would it have to be-- that bigger chip, would also have to be part of a waveguide to lean the modules into them? Yeah, in fact, the waveguide would be running around in that lower-- exactly.
Yeah. Thank you, by the way. Thank you. Thank you.
One of the presentations we saw yesterday, there was a discussion on cosmic radiation, cosmic rays affecting qubits. I know you didn't talk about it here, but I know your group did research on that. I just wanted to find out because I'm doing an article on underground labs to find out are we going to see quantum computers being put underground or are there any new insights you are having? And what could be the impact of cosmic radiation on all these things that you are working on at this point? I'm sorry. I'm having a little trouble hearing.
Could you say it again, please? Oh, I was saying I wanted to-- one of the presenters yesterday, rather, talked about cosmic radiation and its effects on cosmic radiation-- Radiation? Yes. Oh, yeah. I see. Yeah. Cosmic rays, the effect on qubits.
Yeah. And I know your group has done some work in that direction. We have, indeed.
So yeah. So cosmic rays, they're high energy muons by the time they get to us often, and they'll-- they basically cause an earthquake in the substrate, right? It hits the substrate. And that creates phonons, which then interacts with superconductors, creates quasiparticles and quasiparticles take energy from our qubits. And so this happens. And you can see the decay rates immediately go up or the T1's go down.
Worse is that it happens everywhere on the chip. So there's correlated errors. Not only does it happen on qubit 1, but it's going to happen on qubits 1 through 16 at the same time. That's a problem for error correction. So we've done that experiment to show that, that matters. The other experiment we've done is by doing gap engineering of the superconductors, you can make a superconductor thicker or thinner, the film, and that will change its gap, or you could just use a different superconductor, niobium versus aluminum.
And by doing that gap engineering, you can actually prevent the tunneling of quasiparticles across the junction. And so the quasiparticles are still there, the muons are still coming, but the part that takes the energy, the tunneling, we block it. That's very fortunate as otherwise we'd all have to go deep underground. And that probably would prevent commercialization at a large scale of superconducting. So there may be other things that prevent it, but fortunately, cosmic rays probably aren't one of them.
Can we have the next speaker come up? Thank you, Will. Great talk by the way. Many of the processes that you have told us about in this talk rely on having, I would say, perfect control over the relative phases of the two qubit state or many more qubits depending on how we want to scale the system. I wonder what are the main challenges that you experimentally experience when trying to have this relative phase equal to pi over 2 or-- in terms of precision, what are the main challenges that you saw? For-- specifically for controlling those qubits? Yeah, their phases so that we have perfect constructive and destructive interference in one side or the other.
Yeah. So one reason I showed these single qubit gates is because that's an indicator of how well we can do a particular phase, and we'll never do it perfectly. It's only degrees of how close we can get to unity on the fidelity. But if we get close to five 9's, then that means we're limited by other things. And so the single qubit control and some of these phases should at least be at that limit.
Now, there are other phases there, which were related to a two qubit gate, right? And that's another reason why I showed the 99.92% two qubit gate. And we still need to keep improving these fidelities. Fortunately, though, we can implement quantum error correction once these fidelities get to this level or maybe a little bit better. And we need to be at one part in a trillion to do commercial large scale quantum computation, and we very likely will not improve our qubits to one part in a trillion. But we don't have to do that because with quantum error correction, we get exponential reduction in the error rate for only linear or polynomial reductions in the physical qubits.
So if I can make my physical qubit 10x better, depending on the size of my code, I could make my logical error rate orders of magnitude better. And that's very likely how it will happen. Yeah.
Perfect. Thank you. Great. Thanks for the question.
OK. We'll take one more question, and then-- while we switch off the laptops. It's very quick. Thank you. What's the relative benefit of going underground? Thank you. Sorry, my name is Danielle Speller.
Oh. Hi, Danielle. Nice to meet you. You too. What's the relative benefit of going underground versus the mitigation that you found for making that? Yeah, so with these high energy muons or cosmic rays, it turns out you don't have to be just a little bit underground, you have to be way underground.
We're talking, like, deep, deep, deep underground. And so it just becomes impractical to think that we're going to have thousands and thousands of quantum computers that are thousands of feet underground or more, right? Or thousands of meters even. And it just becomes expensive and therefore impractical. And if there were another solution, people would gravitate towards that other solution. So whereas changing the thickness of my metal so that I can do the gap engineering, that's just growing a different thickness metal, and we grow metals all the time. And so it's just it's much easier to do the gap engineering than it is to imagine digging a deep hole or going to a mine or something.
Yeah. Well, I was wondering if you could just give, like, if it's comparable or if the opportunity cost-- we do underground experiments a lot. So-- Oh. --wondering how much you were-- either if you were winning by not doing it at all or if you [INAUDIBLE] within an acceptable-- That's a great question, and I don't have the answer to it.
I think people are doing these experiments right now, both underground and also the gap engineering and both. Some people are doing gap engineering underground, right? So I think it's the full matrix, and we'll see where it lands. I don't know for sure. Thank you. Yeah, thank you for the question.
[INAUDIBLE] OK. There he is. Thank you very much for that wonderful talk and for all the excellent questions given by the audience. Up next, we have Professor Marko Loncar, who is the-- who's a professor of electrical engineering here at Harvard's SEAS, School of Engineering and Applied Sciences. And we will learn about optical interconnects so-- All right.
Hello thanks, everybody, for coming. I'd like to share a few thoughts on optical interconnects that could be used to provide connectivity between various types of qubits, including those that Will just talked about. And I'm going to mention some of these ideas towards the end of the presentation. But basically, this kind of optical interconnect-- and by the way, we are photonics group.
In my group, we study optical communications in classical and quantum domain. And so in classical domain, you know, that whole information technology basically is based on our ability to connect computers and via computers, people and various gadgets using, in particular, optical fiber to go over very long distance. More and more optical fibers and kind of optical communications are finding its way in data centers for enabling larger bandwidth and smaller latency and also reducing the power consumption of data centers because they are actually pretty energy costly. And also actually for wireless communications, like for your cell phones and 5G and emerging application, actually signals are often routed from antennas, from the tower antenna to the base station using optical fiber. So optical communications are essentially everywhere, and that keeps me and my group employed for the most part. But one big issue with these optical communication is security.
And basically the way we send information, for example-- --over long distances, we take laser not too different from the one I'm using here to point on a screen, except it's longer wavelength, so it's not really visible. It's 1.5 micron wavelength, which is where the fiber have very low propagation loss. And then we turn the laser on and off.
And because there's a whole lot of power in this laser signal, somebody could tap in and steal a little bit of light and essentially, eventually break the code we are using, potentially using quantum computers. So apparently, I've been told, that already ongoing is that a lot of the data that's being communicated in classical domain across over long distances, using optical fibers or using lasers, they use various security codes that are very, very hard to decrypt using classical computers. But if you store all of this data and then eventually, you take one of Will's quantum computer, you could potentially decode all of your secrets that you're sending left and right these days. And so the idea is to actually replace these classical communication channel using quantum communication channels that we protected by laws of quantum physics, as essentially, we also use photons like Will.
Our photons would be a much higher energy, so they can propagate with very low loss and very little susceptibility, if any, to noise. And so essentially they can travel quite a distance. And basically then if somebody's eavesdropping, somebody takes your information, if you essentially encode information you're sending in a single photon using the kind of various degrees of freedom of photon, polarization, time frequency, whatnot, you actually can protect this information. So if somebody-- an eavesdropper wants to tap in your communication channel and wants to hear what you're doing, actually you will be immediately able to detect that and stop communication protocol, change the secret key and then continue communicating. And this is kind of one of the ideas, one of the motivations behind this ultimate goal that some of us are aspiring to, which is the quantum internet, which will be kind of quantum version of classical internet that we are all using and love these days.
And so basically here, not only it will be secure, but more importantly, especially in the context of what Will was talking about, if we are to use this quantum internet to connect not classical computer security, but also quantum computers, these links, which will for sure going to be made out of optical fiber. There is some very interesting proposals how this could be done in free space using tunnels of various sorts. But if you stick with optical fiber, then basically what is needed to connect quantum computers to this fiber link, you need essentially quantum modems, right? Just like your electrical computer needs some sort of modem, we call them these days transceivers to take the electrical data to optical domain and back from optical domain back to electrical domain. You will need devices like that in quantum space. And these are called quantum transducers.
And this is one of the things I'm going to tell you about in this presentation. Another component that I'm going to tell you a little bit about, a router components of these components as quantum repeaters. And so these are devices that are there to fight the loss of the optical fiber. So optical fiber is very low loss but even in classical communication world, you cannot propagate forever, and they use a lot of laser power. When your optical signal attenuates-- is it attenuated enough that you can actually not decode information anymore? What you do, you amplify it.
You put an amplifier, erbium doped fiber amplifier, for example, you amplify it, and then you boost your signal, and then you continue propagation. In the quantum world, that's not possible because of essentially no cloning theorem that says you cannot copy quantum information, which is why it's secure in the first place. So what we need are these kind of relays, as I like to refer to them, of quantum information that essentially rely on distributing entanglement over long distance. And so we'll talk quite a bit about entanglement.
And I'm sure I missed a few talks in this conference, but I'm sure there was a lot of entanglement discussion. So your experts on entanglement. So I'm not going to try to explain it.
I wouldn't know how to but anyways. So in order to preserve entanglement, first establish and preserve entanglement, we need to have quantum memories. And so part-- my first part of my talk is going to be focused on these quantum memories. Basically quantum memories that will allow us to make quantum repeaters. And this is a little broader overview, what my group does.
Though, in context of this presentation, mainly I'm talking about photonics that can be used to make quantum memories in diamond. I will not talk at all about ways to use phonons. We'll mention that phonons can be actually really bad for quantum, which is absolutely true.
We are trying to turn this upside down and actually use phonons, us and many other people in the community, use phonons as information carriers to actually try to have them do something useful. But I won't be able to tell you anything about this today. And then the second part, talk a little bit about quantum photonics [INAUDIBLE] material platform we've been working on, it's called thin film lithium niobate.
It's a mouthful, but I'll explain what do we mean by this and why it matters. And then towards the end, unless Bill cuts me off, then I'll tell you a little bit about quantum transduction. Oh, OK. All right. I'll make friends with you. Bill, you don't matter anyway.
OK. All right. So how do we-- how does quantum communication works? How does quantum memory work? Well, basically, we need long lived quantum memory, OK, that can interact with light. So quantum states will be stored in this quantum memory where we are trying to establish entanglement across long distance.
In order-- because atoms are very small and light photons of wavelength, let's say 700 nanometer or ideally 1.5 micron wavelength is pretty large, interaction between light an atom is not very-- OK, here we go-- is not very good. And therefore, we typically put these atoms inside optical resonators so they can actually interact-- the [INAUDIBLE] has higher probability of interacting with an atom. And so this is a node of the quantum network. And so then on the other end, we would have another-- actually, let me throw another node. We have another node of quantum network that also has quantum memory, an atom or it can be, in our case, artificial atom, which is a defect in diamond.
And as long as it can be communicated with using light, we are good. And basically then these two couple using fiber links. To extend coherence, to extend essentially-- to store the information for a longer period of time, we often use also auxiliary memories like a nuclear spin in solid state in our case, whereas this communication memory will be electron spin and diamond.
OK. And so in order for this to work, a few things already are apparent. First, I need to have emitter. I need to have memory that can talk to light.
So that's one thing. Second, I should be able to make very good cavity around this emitter in order to enhance interaction because otherwise interaction is weak. And I need to be able to make two atoms that look almost exactly the same So THAT these photons are all indeed red, right? As illustrated here.
They're the same wavelength, the same frequency. Otherwise, if they have opposite slightly different wavelength, then this communication is not going to happen. And this is actually one thing that's actually pretty hard to do in solid state.
It's very easy to do it with real atoms and trapped ions. It's very hard to do in solid state. It's maybe not so hard to do in superconducting quantum computer because there it is a little bigger-- --but in assistance, we are working with this is actually very difficult. And I'll tell you more about that.
OK. And so our memories, as I mentioned, are cloud centers in diamond. And so thanks to Bob and his wonderful science technology center for a few years ago, we got this beautiful movie from Museum of Science that shows basically the diamond lattice that consist of carbon atoms that then-- --how do we make these defects by essentially we take one carbon atom, replace it with nitrogen, and then nearby carbon atom is knocked out.
This is vacancy and this complex nitrogen vacancy, it becomes actually a negatively charged [INAUDIBLE] electron. This is this cloud. And then we can store information into the spin of this electron. And this is the idea. So now we do not use NV centers anymore. But this is the movie I have.
So what we use is a-- we do have silicon vacancy, but it's not as fancy. We use silicon vacancy. I can tell you why we don't use NV centers in communication. NV centers are very much used in sensing, and they are probably sensing talks here.
And maybe-- I mean, Natalie may talk about NV centers, perhaps. No? OK. All right. So for sensing applications, they're actually workhorse. For quantum communication, we have-- community has switched to silicon vacancy, which basically look more or less the same, except instead of nitrogen, you have silicon and silicon sits between two vacancies, and that's your silicon vacancy center. It has a little better properties.
Oh, wait, wait. These guys-- this is dramatic. Hold on. Let me turn my sound on. So essentially, we don't use commercial diamonds. We use-- well, we don't use man-made-- we don't-- sorry, I go to reset here while doing this.
We don't use natural diamonds. We use man-made diamonds that are commercially available. Though, actually, groups like Tina's group and other groups around the world are-- oh, here we go-- are able to make these very nice, high quality diamonds in a lab. And so basically, what we have, you have methane coming down on diamond substrate and then essentially you lose hydrogen and carbon goes down a lens.
[MUSIC PLAYING] [INAUDIBLE] give me more time to prepare this movie. OK. And so this is a carbon. And then you can dope this chamber with a little bit of nitrogen. Nitrogen. Yeah. And so this is-- and then you need to aneal the whole thing, and you need to actually create some vacancy [INAUDIBLE] centers. So now that we change our-- this is how it looks like when you eliminate nitrogen-- this diamond with nitrogen vacancy center, with green light, you get a lot of red light.
So now that we are using silicon vacancies, I need to make whole new movie. It's probably harder than doing experiments with silicon vacancies. Anyways, so this is how it looks like. But normally when you get these samples-- and this is pink diamond, by the way.
So it's color comes from a bunch of NV's inside. So you can excite them with green and get a lot of red light out. But actually, the problem is that diamond has very high refractive index, so you don't get all these photons out. In fact, only, like, about 5% of light comes out if that much. And so over the years, us and others have looked into ways to improve collection efficiency of light coming out of diamond and in the process, made CNS rich, I'm guessing. I spend-- we are really lucky to have CNS famous.
Famous. OK. Oh, wow. Thank you. And so basically, the first thing that we looked into how we can actually shape these diamonds so that
2024-08-15 17:59


